[數學] 已知方程x^2-11x+(k+30)=0的兩根都比5大，求實數k的取值范圍。(更簡單的解)

題目：已知方程 $x^2-11x+(k+30)=0$ 的兩根都比5大，求實數$k$的取值范圍。
(出處：Facebook 數學問題討論群組)






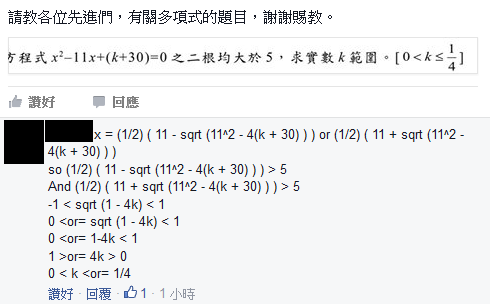
相信大部分人會這樣解：
http://kantiku.com/math-2375322.htm

在FB上回答的人也是：

在此筆者提供另一個解，用到一個小學有學的定理：
等周定理－－等周界的長方形以正方形的面積最大，長方形兩邊長度差越大，面積越小。

設兩根為 $a$ 和 $b$
$a+b=11$ → $b=11-a$ (兩根和)
$a>5$ and $b=11-a>5$
$5<a<6$

$5 \times 6 < ab \leq ( \frac{5+6}{2})^2$ (等周定理)
$30<k+30 \leq (\frac{11}{2})^2$ (兩根積)
$0<k \leq \frac{1}{4}$

在運算上簡單很多。

台灣>國小科展專題<也有等周定理的研究，不過從這專題報告只知道在小學有教，不知是幾年級，筆者之前幫小學生補習時也有看到類似的題目。
 
用到等周定理那一步的合理性可從算幾不等式和二次方程的性質得出：
算幾不等式(AM-HM inequality)
$\frac{a+b}{2} \geq \sqrt{ab}$
$(\frac{11}{2})^2 \geq ab$

$a(11-a)$是開口向下的二次方程，達到極大值時的 $a$ 從算幾不等式可知是 $\frac{11}{2}$，
$a$ 越是離開這點，$a(11-a)$ 則越小，所以 $a(11-a)$ 的極小值是$5 \times 6$

然後兩根積是 $ab=k+30$