[數學] 三角形重心與面積難題

問題：設三角形$ABC$重心為$G$，已知$GA=6$，$GB=9$，$GC=12$。求三角形$ABC$面積。

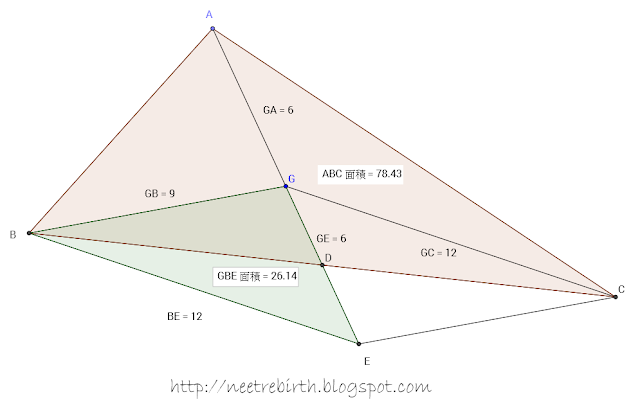
題解：

製圖的時間比解題還長(笑

依題意畫出三角形，然後延長$AG$至$E$點，使得$GA=GE=6$。
$GE$與$BC$相交於$D$點，重心$G$落在中線$AD$上，所以$D$為$BC$的中點
$GD:GA=1:2$   [1]
$GD= \frac{1}{2}GA=3$，$DE=GE-GD=3=GD$
所以$D$亦是$GE$的中點，$GE$與$BC$互相平分，
因此四邊形$BECG$為平行四邊形 (對角線互相平分)

考慮平行四邊形$BECG$
$BE=GC=12$ (對邊相等)

考慮三角形$BEG$ (圖中的綠色三角形)
已知$GB=9$，$GE=6$，$BE=12$
利用希羅公式，定義$s=\frac{GB+GE+BE}{2}=\frac{27}{2}$
面積 $\triangle BEG$
$= \sqrt{s(s-GB)(s-GE)(s-BE)}$
$= \sqrt{s(s-9)(s-6)(s-12)}$
$= \sqrt{\frac{10935}{16}}$
$= \frac{27 \sqrt{15}}{4}$

考慮三角形$ABE$，
$AG:GE=1:1$，由於底邊比等於面積比 [2]，
可知 $\triangle ABG=\triangle BEG=\frac{27 \sqrt{15}}{4}$

由於三角形的重心均分三角形的面績 [3]
所以
$\triangle ABC=3\triangle ABG=3 \frac{27 \sqrt{15}}{4}=\frac{81 \sqrt{15}}{4}$

$\triangle ABC$的面積大約為78.4279。



註解：
[1] 請參考課本重心與中線的章節，或查看可汗學院的>>這個教學(英文)<<
[2] 請參考我之前的文章>>等高三角形的面積比等於底邊比及應用<<
[3] 證明請參考>>這個教學(普通話)<<