[數學] (x^2+3x+1)(x^2+3x+2)+3x^2+9x+2的最小值

問題：求 $(x^2+3x+1)(x^2+3x+2)+3x^2+9x+2$ 的最小值。

剛剛學生傳來問我的，這是嵌套的配方法(Completing the square)題目。
通常看到題中的幾個多項式有大部分係數重覆時，就想想可不可以用另一個代數例如u去取代重覆的部分，然後化簡成平常在解的標準例題形式。

例如本題可這樣解：
$(x^2+3x+1)(x^2+3x+2)+3x^2+9x+2$
$=(x^2+3x+2-1)(x^2+3x+2)+3(x^2+3x+2)-4$
$=u(u-1)+3u-4$, sub. $u=x^2+3x+2$
$=u^2+2u-4$
$(u+1)^2-5$, 配方法

這個的最小值就出現在 $|u+1|$ 達到最小時，
$u+1$
$=x^2+3x+3$
$=(x+3/2)^2+3/4$
很明顯 $u+1$ 的最小值是 $\frac{3}{4}$ 出現在 $x=- \frac{3}{2}$，
要注意，如果 $u+1$ 的最小值小於 $0$，則 $|u+1| $ 的最小值取 $0$。

$(u+1)^2-5$ 的最小值
$=(\frac{3}{4})^2-5$
$=\frac{9}{16}-5$
$=-\frac{71}{16}$

所以 $(x^2+3x+1)(x^2+3x+2)+3x^2+9x+2$ 的最小值為 $-\frac{71}{16}$，出現在 $x=- \frac{3}{2}$。

[數學] 三角形內心與邊長等距應用題

問題：

題解：
$AB=CD=EF$
等弦與圓心等距(eq.chords equidistant from centre)
所以 $O$ 是 $\triangle XYZ$ 的內心(incircle center)。

$OX$ 和 $OY$ 分別平分 $\angle YXZ$ 和 $\angle XYZ$
考慮三角形
$\angle YXO + \angle XYO +121^{\circ}=180^{\circ}$ (三角形內角和)
$\angle YXO + \angle XYO =59^{\circ}$

另外，因為角平分，所以
$\angle YXZ=2\angle YXO$
$\angle XYZ=2\angle XYO$

最後考慮 $\triangle XYZ$
$\angle YXZ+\angle XYZ=2\angle YXO+2\angle XYO$
$\angle YXZ+\angle XYZ=2 \times 59^{\circ}$
$\angle YXZ+\angle XYZ=118^{\circ}$

$\angle YXZ+\angle XYZ +\angle XZY=180^{\circ}$ (三角形內角和)
$118^{\circ} +\angle XZY=180^{\circ}$
$\angle XZY=62^{\circ}$

如果第一步想不到 $O$ 是內心的話似乎也沒法解了。

更新：
其實也是有比較無恥的解法，因為是MC，我不需要知道準確值。
如果 $\angle XOY=120^{\circ}$ 明顯本圖形是旋轉對稱，
三角形 $XYZ$ 是正三角形，$\angle XZY=60^{\circ}$，
固定 $OZ$ 的距離延長 $XY$ 以增加 $\angle XOY$，
可知 $\angle XZY$也會增加，所以 $\angle XOY>60^{\circ}$，
符合條件又接近60度的答案只有B，所以只能是B了。
(還好這題沒有61，63之類的可選)

[數學] 求在單位正方形中, 內切於正方形兩組鄰邊及互相外切的兩圓形的最小面積和

問題：

(出處：Facebook數學討論群組)




題解：
設 $r_1$ 和 $r_2$ 分別是 $O_1$ 和 $O_2$的半徑，
外切點通過圓心至正方形角落的距離為
$(1+\sqrt{2})r$

正方形的對角線長為$\sqrt{2}$

外切點至左下角的距離+外切點至右上角的距離=對角線長
$(1+\sqrt{2})r_1+(1+\sqrt{2})r_2=\sqrt{2}$
$r_1+r_2=\frac{\sqrt{2}}{1+\sqrt{2}}$ ，這是(1)的答案

(2)
$兩圓面積和=(r_1^2+r_2^2)\pi$

根據柯西不等式(Cauchy–Schwarz inequality)
$2(r_1^2+r_2^2) \geq (r_1+r_2)^2$
$(r_1^2+r_2^2) \geq (\frac{1}{1+\sqrt{2}})^2$
$(r_1^2+r_2^2) \geq \frac{1}{3+2\sqrt{2}}$

最小的面積和出現在 $r_1=r_2=r$，其中 $r$ 是常數(可從(1)的答案解出，不過不需要)
所以
$最小面和$ $\\=(r^2+r^2)\pi
\\=\frac{\pi}{3+2\sqrt{2}}$


原發問人是問我怎用梯度(Gradient)和拉格朗日乘數(Lagrange multiplier)去解，
附上該解法：

[數學] 設a>b>c>0, a, b和c屬於整數, (x-c)是f(x)的因式, 其中f(x)=x(x-a)(x-b)-2, 求a+b+c。

問題：設 $a>b>c>0$，a、b和c屬於整數，$(x-c)$ 是 $f(x)$ 的因式，其中 $f(x)=x(x-a)(x-b)-2$，求 $a+b+c$。




題解：

根據餘數定理(Remainder Theorem)
$f(c)=0$
$c(c-a)(c-b)-2=0$
$c(a-c)(b-c)=2$

明顯 $c,(a-c),(b-c)$ 都是正整數，
三個正整數相乘等於 $2$ 的組合只有 ${2,1,1}$

已知 $a>b>c$
所以 $a-c>b-c>0$
可推得
$a-c=2$ 及 $c=b-c=1$
$a=3$ 和 $b=2$

$a+b+c=6$

或者不解出 $a$ 和 $b$，直接求
$a+b+c=a-c+b-c+3c=2+1+3=6$

[數學] 已知方程x^2-11x+(k+30)=0的兩根都比5大，求實數k的取值范圍。(更簡單的解)

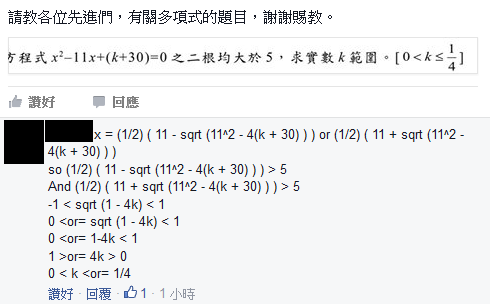
題目：已知方程 $x^2-11x+(k+30)=0$ 的兩根都比5大，求實數$k$的取值范圍。
(出處：Facebook 數學問題討論群組)






相信大部分人會這樣解：
http://kantiku.com/math-2375322.htm

在FB上回答的人也是：

在此筆者提供另一個解，用到一個小學有學的定理：
等周定理－－等周界的長方形以正方形的面積最大，長方形兩邊長度差越大，面積越小。

設兩根為 $a$ 和 $b$
$a+b=11$ → $b=11-a$ (兩根和)
$a>5$ and $b=11-a>5$
$5<a<6$

$5 \times 6 < ab \leq ( \frac{5+6}{2})^2 $ (等周定理)
$30<k+30 \leq (\frac{11}{2})^2$ (兩根積)
$0<k \leq \frac{1}{4}$

在運算上簡單很多。

台灣>國小科展專題<也有等周定理的研究，不過從這專題報告只知道在小學有教，不知是幾年級，筆者之前幫小學生補習時也有看到類似的題目。
 
用到等周定理那一步的合理性可從算幾不等式和二次方程的性質得出：
算幾不等式(AM-HM inequality)
$\frac{a+b}{2} \geq \sqrt{ab}$
$(\frac{11}{2})^2 \geq ab$

$a(11-a)$是開口向下的二次方程，達到極大值時的 $a$ 從算幾不等式可知是 $\frac{11}{2}$，
$a$ 越是離開這點，$a(11-a)$ 則越小，所以 $a(11-a)$ 的極小值是$5 \times 6$

然後兩根積是 $ab=k+30$

[數學] 證明當整數係數多項式f(x)有有理數x=q/p為根時, f(x)/(px+q)也是整係數多項式

最近遇到一位四處向大學教授寄信問數的台灣高中生，他問了我很多大學數學怎算，他會的一些數學方法我也沒看過，感覺真好，有教學相長的感覺。

他問了我一個問題如標題：

出處不明，我的解如下：

根據一次因式檢驗法(Rational root theorem)
$p|a_n=pb_{n-1}→b_{n-1} \in \mathbb{Z}$

其他項則需分析，先展開 $f(x)$：
$f(x)$$\\=(px+q)(b_{n-1}x^{n-1}+b_{n-2}x^{n-2}+...+b_{1}x+b_{0})
\\=(px+q)b_{n-1}x^{n-1}+(px+q)b_{n-2}x^{n-2}+...+(px+q)b_{1}x+(px+q)b_{0}$

設 $g_{i}(x)$$\\= f(x)-(px+q)b_{n-1}x^{n-1}-(px+q)b_{n-2}x^{n-2}-...-(px+q)b_{i+1}x^{i+1}
\\= (px+q)b_{i}x^{i}+(px+q)b_{i-1}x^{i-1}+...+(px+q)b_{1}x+(px+q)b_{0}
\\=pb_{i}x^{i+1}+(pb_{i-1}+qb_{i})x^{i}+...
\\=pb_{i}x^{i+1}+a_{i}x^{i}+...$，$0\leq i \leq n-2$
第二項以後的係數對應 $a_{i} \in \mathbb{Z}$。

設 $b_{i+1}$ 是整數
$a_{i+1}=pb_{i}+qb_{i+1} \in \mathbb{Z}$
則 $pb_{i}=a_{i+1}-qb_{i+1} \in \mathbb{Z}$
$g_{i}(x)$ 的係數為整數。

$g_{i}(x)$ 有因式 $px+q$，
根據一次因式檢驗法(Rational root theorem)
$p|pb_{i}→b_{i} \in \mathbb{Z}$

由 $b_{n-1}$ 為整數，利用數學歸納法可得
$b_{i} \in \mathbb{Z}$, for $0 \leq i \leq n-1$

[數學] 抽球挑戰題(概率)

問題：袋中有2個紅球，3個白球和4個黑球，如每次在袋中抽出一球並不把球放回袋中，紅球先抽完的機率是多少？
(出處忘了，前幾天看到的，但尾指指根關節發炎所以沒發文，還在痛)

剛看到題目的時候沒甚麼頭緒，現在也是，想不到簡明的方法，總之先把我的解法給大家看一下吧：




解：
以R表示紅球，W表示白球，B表示黑球，
把問題轉換成把9球並列，從左算起，兩個R出現在第3個W和第4個B前，
例如
R W W B B B R W B
R W B R W W B B B

設F(n)是符合題目條件，而最後一個R在第n個位置的組合數，
T是9球隨便排列的組合數

$T=9!=362880$

n只可能是2, 3, 4, 5, 6或7，

F(2)表示球以以下方式排列(X表示在第2個R後的球)：
R R X X X X X X X
$F(2)=2!7!=10080$

F(3)表示球以以下方式排列(Y表示在第2個R前非R的球)：
R Y R X X X X X X
Y R R X X X X X X
$F(3)=2!2!6! \times (C^{3}_{1}+C^{4}_{1})=20160$

F(4)表示球以以下方式排列：
R Y Y R X X X X X
...
$F(4)=2!3!5! \times (C^{3}_{2}+C^{3}_{1}C^{4}_{1}+C^{4}_{2})=30240$

F(5)表示球以以下方式排列：
R Y Y Y R X X X X
...
$F(5)=2!4!4! \times (C^{3}_{2}C^{4}_{1}+C^{3}_{1}C^{4}_{2}+C^{4}_{3})=39168$

F(6)表示球以以下方式排列：
R Y Y Y Y R X X X
...
$F(6)=2!5!3! \times (C^{3}_{2}C^{4}_{2}+C^{3}_{1}C^{4}_{3})=43200$

F(7)表示球以以下方式排列：
R Y Y Y Y Y R X X
...
$F(6)=2!6!2! \times (C^{3}_{2}C^{4}_{3})=34560$

所以
$P(先抽完紅色)$$\\ =\frac{F(2)+F(3)+F(4)+F(5)+F(6)+F(7)}{T}
\\ =\frac{177408}{362880}
\\ =\frac{22}{45}$

如果有更好的解法請告訴我。