2015年9月3日 星期四
[數學] 2015遊戲
前兩天在Facebook上看到這個算式,感覺挺有趣的,看起來好像很複雜,實際除了模除外都是中三程度就能處理的,解法如下:
先處理mod前的那串東西,設 $2^{2015}=x$,可得
$\sqrt{(x+x)+(x-x)+(x \times x)+(x \div x)}$
$=\sqrt{x ^2+2x+1}$
$=x+1$
$=2^{2015}+1$
上面一大串只是這樣而已
利用 mod 的性質可得
$2^{2015}+1$ $mod$ $2015$
$=[(2^{2015}$ $mod$ $2015)$ $+(1$ $mod$ $2015)]$ $mod$ $2015$
$=[(2^{13})^{155}$ $mod$ $2015)$ $+1]$ $mod$ $2015$
$=[(2^{13}$ $mod$ $2015)^{155}$ $mod$ $2015$ $+1]$ $mod$ $2015$
$=[11^{155} \times 12^{155}$ $mod$ $2015$ $+1]$ $mod$ $2015$ ------- (1)
感覺好麻煩啊,我先分開算好了,LaTeX碼越來越亂
$[11^{5}$ $mod$ $2015]^{31}$ $mod$ $2015$
$= 1866^{31}$ $mod$ $2015$
$= [(1866^{3}$ $mod$ $2015)^{10}$ $mod$ $2015$ $ \times (1866$ $mod$ $2015)]$ $mod$ $2015$
$= [681^{10}$ $mod$ $2015$ $ \times 1866]$ $mod$ $2015$
$= [[681^{2}$ $mod$ $2015]^5$ $mod$ $2015$ $ \times 1866]$ $mod$ $2015$
$= [311^4$ $mod$ $2015$ $ \times (311 \times 1866)$ $mod$ $2015]$ $mod$ $2015$
$= [(311^2$ $mod$ $2015)^2$ $ \times 6]$ $mod$ $2015$
$= (1 \times 6)$ $mod$ $2015$
$= 6$
我已經開始瘋狂跳步了, 這題目誰設計的啊
$[12^{5}$ $mod$ $2015]^{31}$ $mod$ $2015$
$=987^{31}$ $mod$ $2015$
$=[(987^{3}$ $mod$ $2015)^{10}$ $mod$ $2015$ $\times 987$ $mod$ $2015]$ $mod$ $2015$
$=[1208^{10}$ $mod$ $2015$ $\times 987]$ $mod$ $2015$
$=[(1208^{2}$ $mod$ $2015)^5$ $mod$ $2015$ $\times 987]$ $mod$ $2015$
$=[404^5$ $mod$ $2015$ $\times 987]$ $mod$ $2015$
$=[(404^2$ $mod$ $2015)^2$ $mod$ $2015$ $\times 404 \times 987]$ $mod$ $2015$
$=[1 \times 404 \times 987]$ $mod$ $2015$
$=1793$
把6和1793代回(1)式
$=[6 \times 1793 $mod$ $2015$ $+1]$ $mod$ $2015$
$=(10758 $mod$ $2015$ $+1)$ $mod$ $2015$
$=683+1$ $mod$ $2015$
$=684$
算完,有夠麻煩。
訂閱:
張貼留言
(
Atom
)
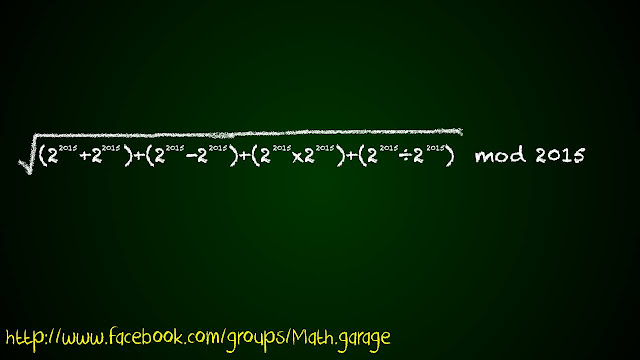
沒有留言 :
張貼留言