問題:
題解:
從圖中兩對同色的相似三角形可證得
$\frac{ZX}{ZA}= \frac{ZY}{ZB}$
故
$XY//AB$
2015年12月14日 星期一
2015年12月10日 星期四
[程式/Mathematica] 沒有row interchange的LU分解函數
首先... SyntaxHighlighter沒法高亮Mathematica的語法,所以下面只能以這種形式表示了
沒有row interchange的LU分解函數(LU Decomposition without row interchanging):
LUFactor[mat0_] :=
Module[{m, n, i, j, k = 1, L, U = mat0},
{m, n} = Dimensions[U];
L = IdentityMatrix[m];
For[j = 1, j < n + 1, j++,
If[U[[k, j]] != 0,
For[i = k + 1, i < m + 1, i++,
L[[i, k]] = U[[i, j]]/U[[k, j]];
U[[i]] = U[[i]] - U[[k]]*U[[i, j]]/U[[k, j]];
];
k++
]
];
Print["L=", L // MatrixForm];
Print["U=", U // MatrixForm];
Return[{L, U}];
]
將這個放在Mathematica的檔案中執行一次後就能呼叫這個函數,在裡面放入要分解的矩陣就可。Print那兩行是顯示L和U,不需要的話可刪除。如果想將這個函數的L和U指定到另外的變數中,可以寫成{a,b}=LUFactor[matrix],這樣L和U就會指定到a和b這兩個變量上。
事源是這樣的,Mathematica本身內置了一個叫LUDecomposition的函數,但它沒法選擇做不做row interchange,而筆者在溫習線性代數的課題時,在LU分解的練習中有些題目是要在不做row interchange的情況下解的,只好放棄。
然後想說其實筆者也會一點編程,應該查一下Mathematica的編程語法就會了吧,於是就邊查邊找別人寫的函數的例子,就編出上面的function了。
一開始只是寫了4x4的矩陣作試驗,然後擴建成nxn,再把參數改一改,令它能處理mxn,最後加一個If和改改參數變成能處理pivot的問題。
不過Mathematica的資料真難找,搜尋常常夾了一堆不相干的東西,像要找function的定義方法就找了很多數學function的相關東西出來,找programming就變mathematical programming,好麻煩。
沒有row interchange的LU分解函數(LU Decomposition without row interchanging):
LUFactor[mat0_] :=
Module[{m, n, i, j, k = 1, L, U = mat0},
{m, n} = Dimensions[U];
L = IdentityMatrix[m];
For[j = 1, j < n + 1, j++,
If[U[[k, j]] != 0,
For[i = k + 1, i < m + 1, i++,
L[[i, k]] = U[[i, j]]/U[[k, j]];
U[[i]] = U[[i]] - U[[k]]*U[[i, j]]/U[[k, j]];
];
k++
]
];
Print["L=", L // MatrixForm];
Print["U=", U // MatrixForm];
Return[{L, U}];
]
將這個放在Mathematica的檔案中執行一次後就能呼叫這個函數,在裡面放入要分解的矩陣就可。Print那兩行是顯示L和U,不需要的話可刪除。如果想將這個函數的L和U指定到另外的變數中,可以寫成{a,b}=LUFactor[matrix],這樣L和U就會指定到a和b這兩個變量上。
事源是這樣的,Mathematica本身內置了一個叫LUDecomposition的函數,但它沒法選擇做不做row interchange,而筆者在溫習線性代數的課題時,在LU分解的練習中有些題目是要在不做row interchange的情況下解的,只好放棄。
然後想說其實筆者也會一點編程,應該查一下Mathematica的編程語法就會了吧,於是就邊查邊找別人寫的函數的例子,就編出上面的function了。
一開始只是寫了4x4的矩陣作試驗,然後擴建成nxn,再把參數改一改,令它能處理mxn,最後加一個If和改改參數變成能處理pivot的問題。
不過Mathematica的資料真難找,搜尋常常夾了一堆不相干的東西,像要找function的定義方法就找了很多數學function的相關東西出來,找programming就變mathematical programming,好麻煩。
標籤:
程式
,
LU
,
Mathematica
2015年12月9日 星期三
[數學] ABCD共圓,AD與BC的延線交於圓外的一點E,BDM為直線,其中MT與圓ABCD相切。若EM//AC,證明MT=ME。
問題:
題解:
Joint $BT$ and $DT$.
Let $MT=a$, $ME=b$, $MD=r$ and $MB=s$
Our aim is to prove $a=b$.
Consider $\triangle BMT$ and $\triangle TMD$,
$\angle BMT= \angle TMB$ (commond $\angle$)
$\angle TBM= \angle DTM$ ($\angle$ in alt. segment)
Thus, $\triangle BMT \sim \triangle TMD$ (AA)
By corr. sides $\sim \triangle s$, we have,
$\begin{align*}
\frac{MT}{MD}&=\frac{MB}{MT}\\
\frac{a}{r}&=\frac{s}{a}\\
a&=\sqrt{rs}
\end{align*}$
Consider $\triangle BME$ and $\triangle EMD$,
$\angle BME= \angle EMD$ (commond $\angle$)
$\angle MBE= \angle A$ ($\angle s$ in the same segment)
$\angle A= \angle MED$ (alt. $\angle s$, $EM//AC$)
so, $\angle MBE= \angle MED$
Thus, $\triangle BME \sim \triangle EMD$ (AA)
By corr. sides $\sim \triangle s$, we have,
$\begin{align*}
\frac{ME}{MD}&=\frac{MB}{ME}\\
\frac{b}{r}&=\frac{s}{b}\\
b&=\sqrt{rs}=a
\end{align*}$
Therefore, $MT=ME$.
$Q.E.D.$
題解:
Joint $BT$ and $DT$.
Let $MT=a$, $ME=b$, $MD=r$ and $MB=s$
Our aim is to prove $a=b$.
Consider $\triangle BMT$ and $\triangle TMD$,
$\angle BMT= \angle TMB$ (commond $\angle$)
$\angle TBM= \angle DTM$ ($\angle$ in alt. segment)
Thus, $\triangle BMT \sim \triangle TMD$ (AA)
By corr. sides $\sim \triangle s$, we have,
$\begin{align*}
\frac{MT}{MD}&=\frac{MB}{MT}\\
\frac{a}{r}&=\frac{s}{a}\\
a&=\sqrt{rs}
\end{align*}$
Consider $\triangle BME$ and $\triangle EMD$,
$\angle BME= \angle EMD$ (commond $\angle$)
$\angle MBE= \angle A$ ($\angle s$ in the same segment)
$\angle A= \angle MED$ (alt. $\angle s$, $EM//AC$)
so, $\angle MBE= \angle MED$
Thus, $\triangle BME \sim \triangle EMD$ (AA)
By corr. sides $\sim \triangle s$, we have,
$\begin{align*}
\frac{ME}{MD}&=\frac{MB}{ME}\\
\frac{b}{r}&=\frac{s}{b}\\
b&=\sqrt{rs}=a
\end{align*}$
Therefore, $MT=ME$.
$Q.E.D.$
2015年12月7日 星期一
[數學] 邊長為a的正方形, 其中三角(逆時針, 從左上開始)至正方形一內點的距離分別為1, 2和3, 求邊長a和對應長度為1和2的線段夾角
問題:
解答:
Let $A:(0,0)$, $B:(0,a)$, $C:(a,a)$, $D:(a,0)$ be the corners of the square.
The equations of the circles centered at $A$, $B$ and $D$ with radii $2$, $1$ and $3$ respectively are
$x^2+y^2=4$ ------- $(1)$
$x^2+y^2-2ay+a^2=1$ ------- $(2)$
$x^2+y^2-2ax+a^2=9$ ------- $(3)$
The point $K:(m,n)$ in the square satisfies these equations simultaneously, where $m>0$ and $n>0$
From (1) and (2), (2) and (3), we have
$2an=a^2+3>0$
$2am=a^2-5>0$
Sum of their squares is
$(2ay)^2+(2ax)^2=4a^2(x^2+y^2)=16a^2$
Thus,
$(a^2+3)^2+(a^2-5)^2=16a^2$
$a^4-10a^2+17=0$
Using quadratic equation to solve $a^2$, which is the area of the square.
$Area=a^2$$\\=\frac{10 \pm \sqrt{10^2-4(17)}}{2}
\\=5 \pm 2 \sqrt{2}
\\=5 + 2 \sqrt{2}$
(Since $a^2>5$, reject $a^2=5-2 \sqrt{2}$)
Therefore $a= \sqrt{5 + 2 \sqrt{2}}$
Consider $\triangle ABK$, by cosine law, we have
$\begin{align*}
a^2&=1^2+2^2-2(1)(2) \cos \theta
\\\cos \theta &=-\frac{1}{\sqrt{2}}
\\\theta &=135 ^\circ
\end{align*}$

P.S. 這個順便測試在Mathb.in寫的東西直接複製過來怎麼,完全沒問題。在Mathb.in編輯簡單多了,寫了的東西可立即顯示,這邊預覽跑半天呢。
解答:
Let $A:(0,0)$, $B:(0,a)$, $C:(a,a)$, $D:(a,0)$ be the corners of the square.
The equations of the circles centered at $A$, $B$ and $D$ with radii $2$, $1$ and $3$ respectively are
$x^2+y^2=4$ ------- $(1)$
$x^2+y^2-2ay+a^2=1$ ------- $(2)$
$x^2+y^2-2ax+a^2=9$ ------- $(3)$
The point $K:(m,n)$ in the square satisfies these equations simultaneously, where $m>0$ and $n>0$
From (1) and (2), (2) and (3), we have
$2an=a^2+3>0$
$2am=a^2-5>0$
Sum of their squares is
$(2ay)^2+(2ax)^2=4a^2(x^2+y^2)=16a^2$
Thus,
$(a^2+3)^2+(a^2-5)^2=16a^2$
$a^4-10a^2+17=0$
Using quadratic equation to solve $a^2$, which is the area of the square.
$Area=a^2$$\\=\frac{10 \pm \sqrt{10^2-4(17)}}{2}
\\=5 \pm 2 \sqrt{2}
\\=5 + 2 \sqrt{2}$
(Since $a^2>5$, reject $a^2=5-2 \sqrt{2}$)
Therefore $a= \sqrt{5 + 2 \sqrt{2}}$
Consider $\triangle ABK$, by cosine law, we have
$\begin{align*}
a^2&=1^2+2^2-2(1)(2) \cos \theta
\\\cos \theta &=-\frac{1}{\sqrt{2}}
\\\theta &=135 ^\circ
\end{align*}$

P.S. 這個順便測試在Mathb.in寫的東西直接複製過來怎麼,完全沒問題。在Mathb.in編輯簡單多了,寫了的東西可立即顯示,這邊預覽跑半天呢。
2015年12月1日 星期二
[電腦] Bluestack 自動下載遊戲 的解決方法
相信有用bluestack的各位應該有被這問題困擾吧?它為了經營而強迫用戶安裝那些apps以收取廣告費,而那些apps總是100Mb上下,很佔電腦資源。筆者搜尋各大中文網站後也沒找到一個簡單又合用的解決方法(一些只是直接推銷其他軟體)。不過在英文網站卻找到了(英文網絡的資源總是比較多呢),簡單,而且目前為止我的bluestack也沒再裝怪apps,事不宜遲,馬上開始:
1. 下載並安裝nova launcher
>>載點<<
nova launcher是啟動android的首頁介面,用它的原因無它,因為所有問題都出在bluestack原來的介面 Gamepop-首頁,所以我們用一個更好的介面取代這個應用。
如果想美化首面,請找有關nova launcher的教學,自己搜尋,我沒需要所以沒弄。
2. 在設定→高級設置→應用程式 中停止並刪除bluestack自帶的apps。
例如 Google Play服務、Gamepop-首頁、Getjar... 總之你覺得沒用的,能刪都刪,不能刪就停用。
3. 重新啟動bluestack,它會問你用甚麼作為首面,你就選永久使用nova launcher。
4. 為防bluestack更新,請編輯登陸檔。
首先在"開始"找regedit.exe,開啟後登錄編輯程式就出來了,然後到
HKEY_LOCAL_MACHINE>SOFTWARE>BlueStacks>Updater
在ManifestURL這個檔上按右鍵,選修改,把原來的網址刪除。
這樣就大功告成了,目前筆者還沒看到bluestack亂裝apps。沒圖沒影片請見諒,因為我不想重做一次,各位請自行嘗試。
1. 下載並安裝nova launcher
>>載點<<
nova launcher是啟動android的首頁介面,用它的原因無它,因為所有問題都出在bluestack原來的介面 Gamepop-首頁,所以我們用一個更好的介面取代這個應用。
如果想美化首面,請找有關nova launcher的教學,自己搜尋,我沒需要所以沒弄。
2. 在設定→高級設置→應用程式 中停止並刪除bluestack自帶的apps。
例如 Google Play服務、Gamepop-首頁、Getjar... 總之你覺得沒用的,能刪都刪,不能刪就停用。
3. 重新啟動bluestack,它會問你用甚麼作為首面,你就選永久使用nova launcher。
4. 為防bluestack更新,請編輯登陸檔。
首先在"開始"找regedit.exe,開啟後登錄編輯程式就出來了,然後到
HKEY_LOCAL_MACHINE>SOFTWARE>BlueStacks>Updater
在ManifestURL這個檔上按右鍵,選修改,把原來的網址刪除。
這樣就大功告成了,目前筆者還沒看到bluestack亂裝apps。沒圖沒影片請見諒,因為我不想重做一次,各位請自行嘗試。
2015年11月30日 星期一
[物理] 平行光進入拋面後, 所有反射光都會通過焦點的數學證明
前設是反射定律。
Consider a general parabola $y^2=4px$.
The focus of the parabola is $(p, 0)$.
Let a general horizontal line be $y=k$, where $k$ is constant.
It cuts the parabola at $( \frac{k^2}{4p}, k)$.
It can be shown that the general normal line at $( \frac{k^2}{4p}, k)$ is:
$y=-\frac{k}{2p}x+k+\frac{k^3}{8p^2}$
and the reflection of the horizontal line through the normal at $( \frac{k^2}{4p}, k)$ is:
$y = -\frac{4pk}{4p^2 - k^2}x + \frac{k^3}{4p^2 - k^2} + k$, where $k \neq 2p$.
Substitute $(p, 0)$ into $y = -\frac{4pk}{4p^2 - k^2}x + \frac{k^3}{4p^2 - k^2} + k$,
we have
$L.H.S=0$
$R.H.S$ $\\=-\frac{4pk}{4p^2 - k^2}p + \frac{k^3}{4p^2 - k^2} + k
\\=\frac{-4p^2k+k^3+4p^2k - k^3}{4p^2 - k^2}
\\=0$
$L.H.S=R.H.S$
for $k=2p$, the reflection line is a vertical line pass through $(p,k)$ and $(p,0)$.
Thus, the reflection line passes the focus.
筆者利用Geogebra將反射的情況畫出來了, 可參考
http://tube.geogebra.org/m/2188507
2015年11月28日 星期六
[數學] 2012 HKDSE MATHS MC 42題 真正秒解
先說說2013年 MC 42題,
Find the range of values of $k$ such that the circle $x^2+y^2+2x-2y-7=0$ and the straight line $3x-4y+k=0$ intersect.
$A.$ $-8<k<22$
$B.$ $-8 \leq k \leq 22$
$C.$ $k<-22$ or $k>8$
$D.$ $k \leq -22$ or $k \geq 8$
k夾在某範圍,可交於一點,必是
$a \leq k \leq b$ 這種形式,B是答案。
而2012年MC42題,在學校沒有教的數學有說明詳解,但他說沒有真正的秒解,所以我這邊就給一個真正的秒解給大家。(這題好像因為命中率低而很紅,網上看到一些補習班數學講座找狀元講解這題)
問題是這樣的:
求 $k$ 值的範圍使得 $x^2+y^2+2x-4y-13=0$ 與直線 $x-y+k=0$ 相交於兩相異點。
$A.$ $-9 < k < 3$
$B.$ $-3 < k < 9$
$C.$ $k<-9$ 或 $k>3$
$D.$ $k < -3$ 或 $k > 9$
有交點,但不能只交於一點,所以必是
$a < k < b$ 這種形式。
圓方程 $x^2+y^2+Dx+Ey+F=0$中,
圓心座標為:$(- \frac{D}{2}, - \frac{E}{2})=(- 1, 2)$
直線方程 $y=mx+c$ 的 $c$ 決定的是線所在的高度,
而圓是對稱的,兩切線中間的平行線必通過圓心,
即對於 $a < k < b$,中間的平行線的 $k$ 值為 $\frac{a+b}{2}$,
所以
$-1-2+\frac{a+b}{2}=0$
$\frac{a+b}{2}=3$
然後很明顯 $\frac{-3+9}{2}=3$
答案是B,不需要二次方程,不需要判別式,
對這題的圖形的圖象有清晰的概念就能解了。
而如果是長題目要找出 $k$ 的上下限,也可以從圖象入手,
我就懶畫了,有興趣請自繪:
圓方程 $x^2+y^2+Dx+Ey+F=0$中,
圓心座標 $(m, n)$ 為:$(- \frac{D}{2}, - \frac{E}{2})=(- 1, 2)$
半徑 $r$ 為 $\frac{1}{2}\sqrt{D^2+E^2-4F}=\frac{1}{2}\sqrt{2^2+4^2-4(-13)}=3\sqrt{2}$
直線 $x-y+k=0$ 的斜率 $s$為 $1$,
考慮三圓心、切點,通過圓心的垂線與切線的交點三者形成的角形,
可知上下限為 $(n-m) \pm \frac{r}{ \sin( \tan^{-1}s)}$,較大的就是上限,較小的是下限。
(這不是通解公式,直線方程我沒用通式,通解請自行推導)
代入可得:
$a$ $\\=(2+1) - \frac{3 \sqrt{2}}{ \sin ( \tan ^{-1}1)} \\
=3 - \frac{3 \sqrt{2} }{ \sin (45^{ \circ})} \\
=3 - \frac{3 \sqrt{2} }{ \frac{1}{ \sqrt{2}}} \\
=3 - 3 \times 2\\
=-3$
$b$ $\\=(2+1) + \frac{3 \sqrt{2}}{ \sin ( \tan ^{-1}1)} \\
=3 + 3 \times 2 \\
=9$
Find the range of values of $k$ such that the circle $x^2+y^2+2x-2y-7=0$ and the straight line $3x-4y+k=0$ intersect.
$A.$ $-8<k<22$
$B.$ $-8 \leq k \leq 22$
$C.$ $k<-22$ or $k>8$
$D.$ $k \leq -22$ or $k \geq 8$
k夾在某範圍,可交於一點,必是
$a \leq k \leq b$ 這種形式,B是答案。
而2012年MC42題,在學校沒有教的數學有說明詳解,但他說沒有真正的秒解,所以我這邊就給一個真正的秒解給大家。(這題好像因為命中率低而很紅,網上看到一些補習班數學講座找狀元講解這題)
問題是這樣的:
求 $k$ 值的範圍使得 $x^2+y^2+2x-4y-13=0$ 與直線 $x-y+k=0$ 相交於兩相異點。
$A.$ $-9 < k < 3$
$B.$ $-3 < k < 9$
$C.$ $k<-9$ 或 $k>3$
$D.$ $k < -3$ 或 $k > 9$
有交點,但不能只交於一點,所以必是
$a < k < b$ 這種形式。
圓方程 $x^2+y^2+Dx+Ey+F=0$中,
圓心座標為:$(- \frac{D}{2}, - \frac{E}{2})=(- 1, 2)$
直線方程 $y=mx+c$ 的 $c$ 決定的是線所在的高度,
而圓是對稱的,兩切線中間的平行線必通過圓心,
即對於 $a < k < b$,中間的平行線的 $k$ 值為 $\frac{a+b}{2}$,
所以
$-1-2+\frac{a+b}{2}=0$
$\frac{a+b}{2}=3$
然後很明顯 $\frac{-3+9}{2}=3$
答案是B,不需要二次方程,不需要判別式,
對這題的圖形的圖象有清晰的概念就能解了。
而如果是長題目要找出 $k$ 的上下限,也可以從圖象入手,
我就懶畫了,有興趣請自繪:
圓方程 $x^2+y^2+Dx+Ey+F=0$中,
圓心座標 $(m, n)$ 為:$(- \frac{D}{2}, - \frac{E}{2})=(- 1, 2)$
半徑 $r$ 為 $\frac{1}{2}\sqrt{D^2+E^2-4F}=\frac{1}{2}\sqrt{2^2+4^2-4(-13)}=3\sqrt{2}$
直線 $x-y+k=0$ 的斜率 $s$為 $1$,
考慮三圓心、切點,通過圓心的垂線與切線的交點三者形成的角形,
可知上下限為 $(n-m) \pm \frac{r}{ \sin( \tan^{-1}s)}$,較大的就是上限,較小的是下限。
(這不是通解公式,直線方程我沒用通式,通解請自行推導)
代入可得:
$a$ $\\=(2+1) - \frac{3 \sqrt{2}}{ \sin ( \tan ^{-1}1)} \\
=3 - \frac{3 \sqrt{2} }{ \sin (45^{ \circ})} \\
=3 - \frac{3 \sqrt{2} }{ \frac{1}{ \sqrt{2}}} \\
=3 - 3 \times 2\\
=-3$
$b$ $\\=(2+1) + \frac{3 \sqrt{2}}{ \sin ( \tan ^{-1}1)} \\
=3 + 3 \times 2 \\
=9$
2015年11月17日 星期二
[數學] 指定期數的分期付款公式
剛剛看到一篇一位補習老師寫的關於分期付款的文章。關於分期付款的介紹請直接到那邊看吧,寫得夠清楚了。但他最後說這不是casio計算機能解的問題,筆者就不太同意了。之前筆者弄過一個[資源/Excel] 貸款供款計算表,裡面用來計算每月供款的公式求法以DSE的課程知識足以求得,而且也是casio能計算的數字。
首先設第 $i$ 期尚欠貸款為 $P_i$ ,$0 \leq i \leq n$,借貸為$P_0$,$P_n=0$
月供 $x$ 元,月利率為 $r$ (即年利率/12), $n$ 為還款期數。
每月的尚欠貸款為上一月的尚欠貸款加上利息再扣除供款:
$P_i=(1+r)P_{i-1}-x$
反覆迭代可得
$P_n=(1+r)^2P_{n-2}-x-x(1+r)$
$P_n=(1+r)^3P_{n-3}-x-x(1+r)-x(1+r)^2$
...
$P_n=(1+r)^nP_0-x(1+(1+r)+(1+r)^2+...+(1+r)^{n-1})$
後面的是等比數列,用DSE教的等比數列和公式可化簡
$P_n=(1+r)^nP_0-x(\frac{(1+r)^{n}-1}{r})$
左方是0,將 $x$ 轉為主項
$x(\frac{(1+r)^{n}-1}{r})=(1+r)^nP_0$
$x=\frac{r(1+r)^n}{(1+r)^{n}-1} P_0$
以該文用的例子來驗算
借貸$=1 200 000$
月利率$= \frac{1.20 \%}{12}=0.001$
還款期數$=20 \times 12=240$
每月供款就會是
$=\frac{0.001(1+0.001)^240}{(1+0.001)^{240}-1} \times 1200000$
$=5626.46$
「每一個數字都不是CASIO這種計算機所能計到」?
上面用的的技巧全都是DSE所需,
迭代考細心
比數列和公式要背
轉換主項中一就學了
最後按計算機應該沒多難吧,CASIO十年前就出了的
可在屏幕編輯算式的計算機很輕鬆就能算出答案了。
首先設第 $i$ 期尚欠貸款為 $P_i$ ,$0 \leq i \leq n$,借貸為$P_0$,$P_n=0$
月供 $x$ 元,月利率為 $r$ (即年利率/12), $n$ 為還款期數。
每月的尚欠貸款為上一月的尚欠貸款加上利息再扣除供款:
$P_i=(1+r)P_{i-1}-x$
反覆迭代可得
$P_n=(1+r)^2P_{n-2}-x-x(1+r)$
$P_n=(1+r)^3P_{n-3}-x-x(1+r)-x(1+r)^2$
...
$P_n=(1+r)^nP_0-x(1+(1+r)+(1+r)^2+...+(1+r)^{n-1})$
後面的是等比數列,用DSE教的等比數列和公式可化簡
$P_n=(1+r)^nP_0-x(\frac{(1+r)^{n}-1}{r})$
左方是0,將 $x$ 轉為主項
$x(\frac{(1+r)^{n}-1}{r})=(1+r)^nP_0$
$x=\frac{r(1+r)^n}{(1+r)^{n}-1} P_0$
以該文用的例子來驗算
借貸$=1 200 000$
月利率$= \frac{1.20 \%}{12}=0.001$
還款期數$=20 \times 12=240$
每月供款就會是
$=\frac{0.001(1+0.001)^240}{(1+0.001)^{240}-1} \times 1200000$
$=5626.46$
「每一個數字都不是CASIO這種計算機所能計到」?
上面用的的技巧全都是DSE所需,
迭代考細心
比數列和公式要背
轉換主項中一就學了
最後按計算機應該沒多難吧,CASIO十年前就出了的
可在屏幕編輯算式的計算機很輕鬆就能算出答案了。
[數學] 54321^2015的最後五位數
問題:
$54321^{2015}$ 的最後五位數。
題解:
老實說我還沒想到比較好的方法,不過 $2^{11}=2048$ ,就算硬解也應該在11步之內能解。
我想過用二項式定理化簡,但步驟數並沒有減少,所以還是放棄了。
利用模除公式
$ab=a \mod 100000+b \mod 100000 \mod 100000$
$54321^{2015}$$\\=(54321^{5})^{403} \mod 100000
\\=75601^{403}
\\=(75601^2)^{201} \cdot 75601
\\=(11201^3)^{67} \cdot 75601
\\=(53601^3)^{22} \cdot 53601 \cdot 75601
\\=40801^{22} \cdot 89201
\\=(40801^3)^7 \cdot 40801 \cdot 89201
\\=42401^7 \cdot 40801 \cdot 89201
\\=56801 \cdot 40801 \cdot 89201
\\=37601 \cdot 89201
\\=46801$
$54321^{2015}$ 的最後五位數。
題解:
老實說我還沒想到比較好的方法,不過 $2^{11}=2048$ ,就算硬解也應該在11步之內能解。
我想過用二項式定理化簡,但步驟數並沒有減少,所以還是放棄了。
利用模除公式
$ab=a \mod 100000+b \mod 100000 \mod 100000$
$54321^{2015}$$\\=(54321^{5})^{403} \mod 100000
\\=75601^{403}
\\=(75601^2)^{201} \cdot 75601
\\=(11201^3)^{67} \cdot 75601
\\=(53601^3)^{22} \cdot 53601 \cdot 75601
\\=40801^{22} \cdot 89201
\\=(40801^3)^7 \cdot 40801 \cdot 89201
\\=42401^7 \cdot 40801 \cdot 89201
\\=56801 \cdot 40801 \cdot 89201
\\=37601 \cdot 89201
\\=46801$
2015年11月12日 星期四
[數學] 設20x^3-21x^2-35x-3之值是3,而24x^3-26x^2-41x-2之值不是4,求x。
看起來雖然不是很像,不過其實這是二次方程!
題解:
$20x^3-21x^2-35x-3=3$
$20x^3-21x^2-35x-6=0$ ...(1)
$24x^3-26x^2-41x-2=4$
$24x^3-26x^2-41x-6=0$ ...(2)
根據題意,表示有些(1)的根不是(2)的根。
如果所有(1)的根都是(2)的根就無解;
如果所有(1)的根都不是(2)的根,
那這題等同在問(1)的所有根,(2)的資料完全沒幫助。
所以合理推測有些(1)的根同時是(2)的根。
先解出同時符合 (1) 和 (2) 的這些根:
這很易解
$6 \times(1)-5 \times(2)$
$4x^2-5x-6=0$
$(4x+3)(x-2)=0$
$x=2$ or $x=-\frac{3}{4}$
再找(1)餘下的根$a$,
可以用長除法,不過既然已有兩根,那根之積(product of roots)會比較快:
$2 \times \frac{-3}{4} \times a= \frac{6}{20}$
$a=- \frac{1}{5}$就是本題所求的根
標籤:
一元二次方程
,
數學
,
DSE
,
quadratic equation
2015年11月5日 星期四
[數學] 整係數多項式帶入分子涉及平方根的數值的速算法 (餘式定理應用)
學生今傳來兩條問題,這類題目我也沒看過,還沒想到更好的解,現分享如下:
假設沒有計算機... 有的話就不用算了。
設
$f(x)=4x^4-8x^3-15x^2+13x+1$
$a= \frac{3+2\sqrt{2}}{2}$
$b= \frac{3-2\sqrt{2}}{2}$
$4(x-a)(x-b)=4x^2-12x+1$
(對比二次方程的兩根和與兩根積)
以 $4x^2-12x+1$ 除
$4x^4-8x^3-15x^2+13x+1$
長除法:
得餘式 2
根據餘式定理,函數 $f(\frac{3+2\sqrt{2}}{2})=2$。
思考方向:
如果可以建立一個有因數 $x-\frac{3+2\sqrt{2}}{2}$ 的整係數多項式,
用它整除原式就可把餘式的因次降下來,
而整係數多項式的長除法也相對簡單。
$\frac{3+2\sqrt{2}}{2}$ 類似二次方程的通解,
對比下可設正負開方為兩根,得整係數二次多項式,
用它除原式得一因次最大為1的餘數多項式。
同類題目可用同樣解法:
設
$m=\frac{1+\sqrt{5}}{2}$
$n=\frac{1-\sqrt{5}}{2}$
$(x-m)(x-n)=x^2-x-1$
以 $x^2-x-1$ 除
$8x^3-16x^2+2x+15$
得餘式 $2x+7$
代入 $x=\frac{1+\sqrt{5}}{2}$
得解為 $1+\sqrt{5}+7=8+ \sqrt{5}$
所以 $(a, b)=(8, 1)$
對於3以下的因次,這做法其實也沒多快,但對於6次以上的多項式,這方法的速度優勢就很明顯了,畢竟長除法只是整數加減,但 $(a+b\sqrt{c})^n$ 卻要比較沒開開的常數和有關方的係數。
假設沒有計算機... 有的話就不用算了。
設
$f(x)=4x^4-8x^3-15x^2+13x+1$
$a= \frac{3+2\sqrt{2}}{2}$
$b= \frac{3-2\sqrt{2}}{2}$
$4(x-a)(x-b)=4x^2-12x+1$
(對比二次方程的兩根和與兩根積)
以 $4x^2-12x+1$ 除
$4x^4-8x^3-15x^2+13x+1$
長除法:
得餘式 2
根據餘式定理,函數 $f(\frac{3+2\sqrt{2}}{2})=2$。
思考方向:
如果可以建立一個有因數 $x-\frac{3+2\sqrt{2}}{2}$ 的整係數多項式,
用它整除原式就可把餘式的因次降下來,
而整係數多項式的長除法也相對簡單。
$\frac{3+2\sqrt{2}}{2}$ 類似二次方程的通解,
對比下可設正負開方為兩根,得整係數二次多項式,
用它除原式得一因次最大為1的餘數多項式。
同類題目可用同樣解法:
設
$m=\frac{1+\sqrt{5}}{2}$
$n=\frac{1-\sqrt{5}}{2}$
$(x-m)(x-n)=x^2-x-1$
以 $x^2-x-1$ 除
$8x^3-16x^2+2x+15$
得餘式 $2x+7$
代入 $x=\frac{1+\sqrt{5}}{2}$
得解為 $1+\sqrt{5}+7=8+ \sqrt{5}$
所以 $(a, b)=(8, 1)$
對於3以下的因次,這做法其實也沒多快,但對於6次以上的多項式,這方法的速度優勢就很明顯了,畢竟長除法只是整數加減,但 $(a+b\sqrt{c})^n$ 卻要比較沒開開的常數和有關方的係數。
標籤:
數學
,
餘式定理
,
DSE
,
Maths
,
Remainder Theorem
2015年11月4日 星期三
[數學] (x^2+3x+1)(x^2+3x+2)+3x^2+9x+2的最小值
問題:求 $(x^2+3x+1)(x^2+3x+2)+3x^2+9x+2$ 的最小值。
剛剛學生傳來問我的,這是嵌套的配方法(Completing the square)題目。
通常看到題中的幾個多項式有大部分係數重覆時,就想想可不可以用另一個代數例如u去取代重覆的部分,然後化簡成平常在解的標準例題形式。
例如本題可這樣解:
$(x^2+3x+1)(x^2+3x+2)+3x^2+9x+2$
$=(x^2+3x+2-1)(x^2+3x+2)+3(x^2+3x+2)-4$
$=u(u-1)+3u-4$, sub. $u=x^2+3x+2$
$=u^2+2u-4$
$(u+1)^2-5$, 配方法
這個的最小值就出現在 $|u+1|$ 達到最小時,
$u+1$
$=x^2+3x+3$
$=(x+3/2)^2+3/4$
很明顯 $u+1$ 的最小值是 $\frac{3}{4}$ 出現在 $x=- \frac{3}{2}$,
要注意,如果 $u+1$ 的最小值小於 $0$,則 $|u+1| $ 的最小值取 $0$。
$(u+1)^2-5$ 的最小值
$=(\frac{3}{4})^2-5$
$=\frac{9}{16}-5$
$=-\frac{71}{16}$
所以 $(x^2+3x+1)(x^2+3x+2)+3x^2+9x+2$ 的最小值為 $-\frac{71}{16}$,出現在 $x=- \frac{3}{2}$。
剛剛學生傳來問我的,這是嵌套的配方法(Completing the square)題目。
通常看到題中的幾個多項式有大部分係數重覆時,就想想可不可以用另一個代數例如u去取代重覆的部分,然後化簡成平常在解的標準例題形式。
例如本題可這樣解:
$(x^2+3x+1)(x^2+3x+2)+3x^2+9x+2$
$=(x^2+3x+2-1)(x^2+3x+2)+3(x^2+3x+2)-4$
$=u(u-1)+3u-4$, sub. $u=x^2+3x+2$
$=u^2+2u-4$
$(u+1)^2-5$, 配方法
這個的最小值就出現在 $|u+1|$ 達到最小時,
$u+1$
$=x^2+3x+3$
$=(x+3/2)^2+3/4$
很明顯 $u+1$ 的最小值是 $\frac{3}{4}$ 出現在 $x=- \frac{3}{2}$,
要注意,如果 $u+1$ 的最小值小於 $0$,則 $|u+1| $ 的最小值取 $0$。
$(u+1)^2-5$ 的最小值
$=(\frac{3}{4})^2-5$
$=\frac{9}{16}-5$
$=-\frac{71}{16}$
所以 $(x^2+3x+1)(x^2+3x+2)+3x^2+9x+2$ 的最小值為 $-\frac{71}{16}$,出現在 $x=- \frac{3}{2}$。
標籤:
配方法
,
數學
,
Completing the square
,
DSE
2015年11月1日 星期日
[數學] 三角形內心與邊長等距應用題
問題:
題解:
$AB=CD=EF$
等弦與圓心等距(eq.chords equidistant from centre)
所以 $O$ 是 $\triangle XYZ$ 的內心(incircle center)。
$OX$ 和 $OY$ 分別平分 $\angle YXZ$ 和 $\angle XYZ$
考慮三角形
$\angle YXO + \angle XYO +121^{\circ}=180^{\circ}$ (三角形內角和)
$\angle YXO + \angle XYO =59^{\circ}$
另外,因為角平分,所以
$\angle YXZ=2\angle YXO$
$\angle XYZ=2\angle XYO$
最後考慮 $\triangle XYZ$
$\angle YXZ+\angle XYZ=2\angle YXO+2\angle XYO$
$\angle YXZ+\angle XYZ=2 \times 59^{\circ}$
$\angle YXZ+\angle XYZ=118^{\circ}$
$\angle YXZ+\angle XYZ +\angle XZY=180^{\circ}$ (三角形內角和)
$118^{\circ} +\angle XZY=180^{\circ}$
$\angle XZY=62^{\circ}$
如果第一步想不到 $O$ 是內心的話似乎也沒法解了。
更新:
其實也是有比較無恥的解法,因為是MC,我不需要知道準確值。
如果 $\angle XOY=120^{\circ}$ 明顯本圖形是旋轉對稱,
三角形 $XYZ$ 是正三角形,$\angle XZY=60^{\circ}$,
固定 $OZ$ 的距離延長 $XY$ 以增加 $\angle XOY$,
可知 $\angle XZY$也會增加,所以 $\angle XOY>60^{\circ}$,
符合條件又接近60度的答案只有B,所以只能是B了。
(還好這題沒有61,63之類的可選)
題解:
$AB=CD=EF$
等弦與圓心等距(eq.chords equidistant from centre)
所以 $O$ 是 $\triangle XYZ$ 的內心(incircle center)。
$OX$ 和 $OY$ 分別平分 $\angle YXZ$ 和 $\angle XYZ$
考慮三角形
$\angle YXO + \angle XYO +121^{\circ}=180^{\circ}$ (三角形內角和)
$\angle YXO + \angle XYO =59^{\circ}$
另外,因為角平分,所以
$\angle YXZ=2\angle YXO$
$\angle XYZ=2\angle XYO$
最後考慮 $\triangle XYZ$
$\angle YXZ+\angle XYZ=2\angle YXO+2\angle XYO$
$\angle YXZ+\angle XYZ=2 \times 59^{\circ}$
$\angle YXZ+\angle XYZ=118^{\circ}$
$\angle YXZ+\angle XYZ +\angle XZY=180^{\circ}$ (三角形內角和)
$118^{\circ} +\angle XZY=180^{\circ}$
$\angle XZY=62^{\circ}$
如果第一步想不到 $O$ 是內心的話似乎也沒法解了。
更新:
其實也是有比較無恥的解法,因為是MC,我不需要知道準確值。
如果 $\angle XOY=120^{\circ}$ 明顯本圖形是旋轉對稱,
三角形 $XYZ$ 是正三角形,$\angle XZY=60^{\circ}$,
固定 $OZ$ 的距離延長 $XY$ 以增加 $\angle XOY$,
可知 $\angle XZY$也會增加,所以 $\angle XOY>60^{\circ}$,
符合條件又接近60度的答案只有B,所以只能是B了。
(還好這題沒有61,63之類的可選)
2015年10月29日 星期四
[數學] 求在單位正方形中, 內切於正方形兩組鄰邊及互相外切的兩圓形的最小面積和
問題:
(出處:Facebook數學討論群組)
題解:
設 $r_1$ 和 $r_2$ 分別是 $O_1$ 和 $O_2$的半徑,
外切點通過圓心至正方形角落的距離為
$(1+\sqrt{2})r$
正方形的對角線長為$\sqrt{2}$
外切點至左下角的距離+外切點至右上角的距離=對角線長
$(1+\sqrt{2})r_1+(1+\sqrt{2})r_2=\sqrt{2}$
$r_1+r_2=\frac{\sqrt{2}}{1+\sqrt{2}}$ ,這是(1)的答案
(2)
$兩圓面積和=(r_1^2+r_2^2)\pi$
根據柯西不等式(Cauchy–Schwarz inequality)
$2(r_1^2+r_2^2) \geq (r_1+r_2)^2$
$(r_1^2+r_2^2) \geq (\frac{1}{1+\sqrt{2}})^2$
$(r_1^2+r_2^2) \geq \frac{1}{3+2\sqrt{2}}$
最小的面積和出現在 $r_1=r_2=r$,其中 $r$ 是常數(可從(1)的答案解出,不過不需要)
所以
$最小面和$ $\\=(r^2+r^2)\pi
\\=\frac{\pi}{3+2\sqrt{2}}$
原發問人是問我怎用梯度(Gradient)和拉格朗日乘數(Lagrange multiplier)去解,
附上該解法:
題解:
設 $r_1$ 和 $r_2$ 分別是 $O_1$ 和 $O_2$的半徑,
外切點通過圓心至正方形角落的距離為
$(1+\sqrt{2})r$
正方形的對角線長為$\sqrt{2}$
外切點至左下角的距離+外切點至右上角的距離=對角線長
$(1+\sqrt{2})r_1+(1+\sqrt{2})r_2=\sqrt{2}$
$r_1+r_2=\frac{\sqrt{2}}{1+\sqrt{2}}$ ,這是(1)的答案
(2)
$兩圓面積和=(r_1^2+r_2^2)\pi$
根據柯西不等式(Cauchy–Schwarz inequality)
$2(r_1^2+r_2^2) \geq (r_1+r_2)^2$
$(r_1^2+r_2^2) \geq (\frac{1}{1+\sqrt{2}})^2$
$(r_1^2+r_2^2) \geq \frac{1}{3+2\sqrt{2}}$
最小的面積和出現在 $r_1=r_2=r$,其中 $r$ 是常數(可從(1)的答案解出,不過不需要)
所以
$最小面和$ $\\=(r^2+r^2)\pi
\\=\frac{\pi}{3+2\sqrt{2}}$
原發問人是問我怎用梯度(Gradient)和拉格朗日乘數(Lagrange multiplier)去解,
附上該解法:
[數學] 設a>b>c>0, a, b和c屬於整數, (x-c)是f(x)的因式, 其中f(x)=x(x-a)(x-b)-2, 求a+b+c。
問題:設 $a>b>c>0$,a、b和c屬於整數,$(x-c)$ 是 $f(x)$ 的因式,其中 $f(x)=x(x-a)(x-b)-2$,求 $a+b+c$。
題解:
根據餘數定理(Remainder Theorem)
$f(c)=0$
$c(c-a)(c-b)-2=0$
$c(a-c)(b-c)=2$
明顯 $c,(a-c),(b-c)$ 都是正整數,
三個正整數相乘等於 $2$ 的組合只有 ${2,1,1}$
已知 $a>b>c$
所以 $a-c>b-c>0$
可推得
$a-c=2$ 及 $c=b-c=1$
$a=3$ 和 $b=2$
$a+b+c=6$
或者不解出 $a$ 和 $b$,直接求
$a+b+c=a-c+b-c+3c=2+1+3=6$
題解:
根據餘數定理(Remainder Theorem)
$f(c)=0$
$c(c-a)(c-b)-2=0$
$c(a-c)(b-c)=2$
明顯 $c,(a-c),(b-c)$ 都是正整數,
三個正整數相乘等於 $2$ 的組合只有 ${2,1,1}$
已知 $a>b>c$
所以 $a-c>b-c>0$
可推得
$a-c=2$ 及 $c=b-c=1$
$a=3$ 和 $b=2$
$a+b+c=6$
或者不解出 $a$ 和 $b$,直接求
$a+b+c=a-c+b-c+3c=2+1+3=6$
標籤:
數學
,
餘數定理
,
DSE
,
Remainder Theorem
2015年10月28日 星期三
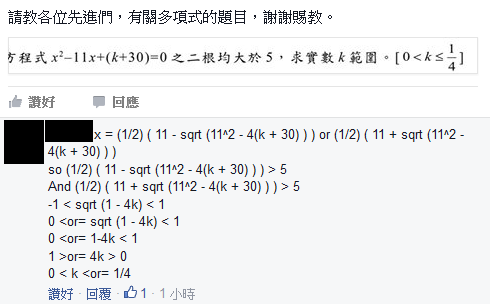
[數學] 已知方程x^2-11x+(k+30)=0的兩根都比5大,求實數k的取值范圍。(更簡單的解)
題目:已知方程 $x^2-11x+(k+30)=0$ 的兩根都比5大,求實數$k$的取值范圍。
(出處:Facebook 數學問題討論群組)
相信大部分人會這樣解:
http://kantiku.com/math-2375322.htm
在FB上回答的人也是:
在此筆者提供另一個解,用到一個小學有學的定理:
等周定理--等周界的長方形以正方形的面積最大,長方形兩邊長度差越大,面積越小。
設兩根為 $a$ 和 $b$
$a+b=11$ → $b=11-a$ (兩根和)
$a>5$ and $b=11-a>5$
$5<a<6$
$5 \times 6 < ab \leq ( \frac{5+6}{2})^2 $ (等周定理)
$30<k+30 \leq (\frac{11}{2})^2$ (兩根積)
$0<k \leq \frac{1}{4}$
在運算上簡單很多。
台灣>國小科展專題<也有等周定理的研究,不過從這專題報告只知道在小學有教,不知是幾年級,筆者之前幫小學生補習時也有看到類似的題目。
用到等周定理那一步的合理性可從算幾不等式和二次方程的性質得出:
算幾不等式(AM-HM inequality)
$\frac{a+b}{2} \geq \sqrt{ab}$
$(\frac{11}{2})^2 \geq ab$
$a(11-a)$是開口向下的二次方程,達到極大值時的 $a$ 從算幾不等式可知是 $\frac{11}{2}$,
$a$ 越是離開這點,$a(11-a)$ 則越小,所以 $a(11-a)$ 的極小值是$5 \times 6$
然後兩根積是 $ab=k+30$
(出處:Facebook 數學問題討論群組)
相信大部分人會這樣解:
http://kantiku.com/math-2375322.htm
在FB上回答的人也是:
在此筆者提供另一個解,用到一個小學有學的定理:
等周定理--等周界的長方形以正方形的面積最大,長方形兩邊長度差越大,面積越小。
設兩根為 $a$ 和 $b$
$a+b=11$ → $b=11-a$ (兩根和)
$a>5$ and $b=11-a>5$
$5<a<6$
$5 \times 6 < ab \leq ( \frac{5+6}{2})^2 $ (等周定理)
$30<k+30 \leq (\frac{11}{2})^2$ (兩根積)
$0<k \leq \frac{1}{4}$
在運算上簡單很多。
台灣>國小科展專題<也有等周定理的研究,不過從這專題報告只知道在小學有教,不知是幾年級,筆者之前幫小學生補習時也有看到類似的題目。
用到等周定理那一步的合理性可從算幾不等式和二次方程的性質得出:
算幾不等式(AM-HM inequality)
$\frac{a+b}{2} \geq \sqrt{ab}$
$(\frac{11}{2})^2 \geq ab$
$a(11-a)$是開口向下的二次方程,達到極大值時的 $a$ 從算幾不等式可知是 $\frac{11}{2}$,
$a$ 越是離開這點,$a(11-a)$ 則越小,所以 $a(11-a)$ 的極小值是$5 \times 6$
然後兩根積是 $ab=k+30$
2015年10月26日 星期一
[數學] 證明當整數係數多項式f(x)有有理數x=q/p為根時, f(x)/(px+q)也是整係數多項式
最近遇到一位四處向大學教授寄信問數的台灣高中生,他問了我很多大學數學怎算,他會的一些數學方法我也沒看過,感覺真好,有教學相長的感覺。
他問了我一個問題如標題:
出處不明,我的解如下:
根據一次因式檢驗法(Rational root theorem)
$p|a_n=pb_{n-1}→b_{n-1} \in \mathbb{Z}$
其他項則需分析,先展開 $f(x)$:
$f(x)$$\\=(px+q)(b_{n-1}x^{n-1}+b_{n-2}x^{n-2}+...+b_{1}x+b_{0})
\\=(px+q)b_{n-1}x^{n-1}+(px+q)b_{n-2}x^{n-2}+...+(px+q)b_{1}x+(px+q)b_{0}$
設 $g_{i}(x)$$\\= f(x)-(px+q)b_{n-1}x^{n-1}-(px+q)b_{n-2}x^{n-2}-...-(px+q)b_{i+1}x^{i+1}
\\= (px+q)b_{i}x^{i}+(px+q)b_{i-1}x^{i-1}+...+(px+q)b_{1}x+(px+q)b_{0}
\\=pb_{i}x^{i+1}+(pb_{i-1}+qb_{i})x^{i}+...
\\=pb_{i}x^{i+1}+a_{i}x^{i}+...$,$0\leq i \leq n-2$
第二項以後的係數對應 $a_{i} \in \mathbb{Z}$。
設 $b_{i+1}$ 是整數
$a_{i+1}=pb_{i}+qb_{i+1} \in \mathbb{Z}$
則 $pb_{i}=a_{i+1}-qb_{i+1} \in \mathbb{Z}$
$g_{i}(x)$ 的係數為整數。
$g_{i}(x)$ 有因式 $px+q$,
根據一次因式檢驗法(Rational root theorem)
$p|pb_{i}→b_{i} \in \mathbb{Z}$
由 $b_{n-1}$ 為整數,利用數學歸納法可得
$b_{i} \in \mathbb{Z}$, for $0 \leq i \leq n-1$
標籤:
多項式
,
數學
,
Polynomial
2015年10月24日 星期六
[數學] 抽球挑戰題(概率)
問題:袋中有2個紅球,3個白球和4個黑球,如每次在袋中抽出一球並不把球放回袋中,紅球先抽完的機率是多少?
(出處忘了,前幾天看到的,但尾指指根關節發炎所以沒發文,還在痛)
剛看到題目的時候沒甚麼頭緒,現在也是,想不到簡明的方法,總之先把我的解法給大家看一下吧:
解:
以R表示紅球,W表示白球,B表示黑球,
把問題轉換成把9球並列,從左算起,兩個R出現在第3個W和第4個B前,
例如
R W W B B B R W B
R W B R W W B B B
設F(n)是符合題目條件,而最後一個R在第n個位置的組合數,
T是9球隨便排列的組合數
$T=9!=362880$
n只可能是2, 3, 4, 5, 6或7,
F(2)表示球以以下方式排列(X表示在第2個R後的球):
R R X X X X X X X
$F(2)=2!7!=10080$
F(3)表示球以以下方式排列(Y表示在第2個R前非R的球):
R Y R X X X X X X
Y R R X X X X X X
$F(3)=2!2!6! \times (C^{3}_{1}+C^{4}_{1})=20160$
F(4)表示球以以下方式排列:
R Y Y R X X X X X
...
$F(4)=2!3!5! \times (C^{3}_{2}+C^{3}_{1}C^{4}_{1}+C^{4}_{2})=30240$
F(5)表示球以以下方式排列:
R Y Y Y R X X X X
...
$F(5)=2!4!4! \times (C^{3}_{2}C^{4}_{1}+C^{3}_{1}C^{4}_{2}+C^{4}_{3})=39168$
F(6)表示球以以下方式排列:
R Y Y Y Y R X X X
...
$F(6)=2!5!3! \times (C^{3}_{2}C^{4}_{2}+C^{3}_{1}C^{4}_{3})=43200$
F(7)表示球以以下方式排列:
R Y Y Y Y Y R X X
...
$F(6)=2!6!2! \times (C^{3}_{2}C^{4}_{3})=34560$
所以
$P(先抽完紅色)$$\\ =\frac{F(2)+F(3)+F(4)+F(5)+F(6)+F(7)}{T}
\\ =\frac{177408}{362880}
\\ =\frac{22}{45}$
如果有更好的解法請告訴我。
(出處忘了,前幾天看到的,但尾指指根關節發炎所以沒發文,還在痛)
剛看到題目的時候沒甚麼頭緒,現在也是,想不到簡明的方法,總之先把我的解法給大家看一下吧:
解:
以R表示紅球,W表示白球,B表示黑球,
把問題轉換成把9球並列,從左算起,兩個R出現在第3個W和第4個B前,
例如
R W W B B B R W B
R W B R W W B B B
設F(n)是符合題目條件,而最後一個R在第n個位置的組合數,
T是9球隨便排列的組合數
$T=9!=362880$
n只可能是2, 3, 4, 5, 6或7,
F(2)表示球以以下方式排列(X表示在第2個R後的球):
R R X X X X X X X
$F(2)=2!7!=10080$
F(3)表示球以以下方式排列(Y表示在第2個R前非R的球):
R Y R X X X X X X
Y R R X X X X X X
$F(3)=2!2!6! \times (C^{3}_{1}+C^{4}_{1})=20160$
F(4)表示球以以下方式排列:
R Y Y R X X X X X
...
$F(4)=2!3!5! \times (C^{3}_{2}+C^{3}_{1}C^{4}_{1}+C^{4}_{2})=30240$
F(5)表示球以以下方式排列:
R Y Y Y R X X X X
...
$F(5)=2!4!4! \times (C^{3}_{2}C^{4}_{1}+C^{3}_{1}C^{4}_{2}+C^{4}_{3})=39168$
F(6)表示球以以下方式排列:
R Y Y Y Y R X X X
...
$F(6)=2!5!3! \times (C^{3}_{2}C^{4}_{2}+C^{3}_{1}C^{4}_{3})=43200$
F(7)表示球以以下方式排列:
R Y Y Y Y Y R X X
...
$F(6)=2!6!2! \times (C^{3}_{2}C^{4}_{3})=34560$
所以
$P(先抽完紅色)$$\\ =\frac{F(2)+F(3)+F(4)+F(5)+F(6)+F(7)}{T}
\\ =\frac{177408}{362880}
\\ =\frac{22}{45}$
如果有更好的解法請告訴我。
2015年10月13日 星期二
[數學] 一元二次方程 (quadratic equation) 挑戰題
題目:
甲乙兩人用公式解一元二次方程式 $x^2 + bx + c = 0$, 甲錯算 $b^2 - 4c$ 得兩根 $(3, -2)$,乙錯看 $b$ 得兩根 $(-5, 2)$,則原方程式為?
(出自:https://www.ptt.cc/bbs/tutor/M.1263636512.A.D15.html)
[原題是 $x^2 + bx + c = 0$,但這沒意義,三個未知數,兩條式,也就是最少有一個是自由變數(free variable),不失一般性(WLOG) ,設$a$為$1$]
題解:
兩根和$=-b$
兩根積$=c$
二次方程公式解$x=\frac{-b \pm \sqrt{b^2-4c}}{2}$
1. 甲算錯 $b^2 - 4c$ 並不影響兩根之和,因為從公式可知在計算兩根和時 $b^2 - 4c$ 這一項會一加一減相消,也就是甲所得到的根可算出正確的兩根和,即
$-b$ $=3-2\\
=1$
$b=-1$
2. 同理,乙錯看 $b$ 並不影響兩根積,即
$c$ $\\=-5 \times 2
\\=-10$
所以原方程為 $x^2 - x - 10 = 0$
甲乙兩人用公式解一元二次方程式 $x^2 + bx + c = 0$, 甲錯算 $b^2 - 4c$ 得兩根 $(3, -2)$,乙錯看 $b$ 得兩根 $(-5, 2)$,則原方程式為?
(出自:https://www.ptt.cc/bbs/tutor/M.1263636512.A.D15.html)
[原題是 $x^2 + bx + c = 0$,但這沒意義,三個未知數,兩條式,也就是最少有一個是自由變數(free variable),不失一般性(WLOG) ,設$a$為$1$]
題解:
兩根和$=-b$
兩根積$=c$
二次方程公式解$x=\frac{-b \pm \sqrt{b^2-4c}}{2}$
1. 甲算錯 $b^2 - 4c$ 並不影響兩根之和,因為從公式可知在計算兩根和時 $b^2 - 4c$ 這一項會一加一減相消,也就是甲所得到的根可算出正確的兩根和,即
$-b$ $=3-2\\
=1$
$b=-1$
2. 同理,乙錯看 $b$ 並不影響兩根積,即
$c$ $\\=-5 \times 2
\\=-10$
所以原方程為 $x^2 - x - 10 = 0$
標籤:
一元二次方程
,
數學
,
DSE
,
Maths
,
quadratic equation
2015年10月11日 星期日
[數學] 面積趣題 (限時1分鐘)
(原圖是打橫的,不知怎麼上傳就變成打直了,真怪,不過不影響問題就算了。)
(問題來自https://brilliant.org/)
... ... ...
... ...
...
..
.
答案:一樣大
解:
設最大的圓的面積是4X,
中圓的面積則是X (長度比的平方等於面積比),
黃色部分面積是Y。
利算排容原理(Inclusion–exclusion principle)可知
藍色部分面積
$\\=大圓-4 \times小圓+黃色部分
\\=4X-4\times X+Y
\\=Y
\\=黃色部分面積$
排容原理在比較深的機率和算組合數的題目中很常用,把這種面積重疊問題想成范氏圖(Venn Diagram)的話就不難理解兩者的關係了。一般兩圖形重疊的情況直接想也想得出怎算,但重疊三次以上的圖就不那麼好想了,引用排容原理能快速解題。
標籤:
范氏圖
,
面積
,
排容原理
,
數學
,
機率
,
DSE
,
Inclusion–exclusion principle
,
Maths
,
Venn Diagram
2015年10月10日 星期六
[科學] 植物會痛嗎?
Do plants feel pain?
重點整理:
1. 切開植物所散發的氣味,像剪草的草青味,是來自植物受到威脅(感到恐懼)時的化學反應(防衛機制)。
2. 不同植物有不同的反應,甚至會有通過這些反應通知同伴和拯救同伴的行為。例如一些植物受攻擊時,它會放出一些化學物質(氣體),接收到這些物質的同種植物也會作出相同的反應。
3. 這些化學物質效果各異,有些可令攻擊者中毒,有些可吸引具攻擊性的昆蟲過來以驅趕攻擊者。例如植物會釋出咖啡因吸引蜜蜂保護自己。
4. 德國波昂大學的研究指出植物放出氣體並發出一些人類無法聽見的聲音的行為等同人類的哭泣。當花、草青瓜受傷時會有這些反應。而美國密蘇里大學的研究進一步指出,當在植物前播放毛蟲吃它的同類的聲音,它們也會"哭泣",表示植物有分辨、認知同伴慘遭毒手的能力。
5. 植物縱然沒腦,但也有智能的表現,例如改變生長的方向繞過障礙物;在受到昆蟲襲擊時通知同伴等。
6. 通過追蹤含放射性碳元素的肥料的粒子流向,研究員發現樹木會和30平方米內的其他樹形成互相溝通的網絡,並利用它們的根把養份輸送到幼小的樹木,直至它長得夠高,能進行光合作用為止。(可比擬人類育嬰)
個人感想:
沒有生物傾向追求死亡,所有生物都為了生存而努力,一些總是以素食者自居,高高在上地批評其他人食肉殘忍的時候,只不過是他們無視了植物的叫聲,或者冤枉植物沒有痛覺,既然要選擇性無視植物的想法,那何不乾脆點,君子遠刨廚就好了吧。
重點整理:
1. 切開植物所散發的氣味,像剪草的草青味,是來自植物受到威脅(感到恐懼)時的化學反應(防衛機制)。
2. 不同植物有不同的反應,甚至會有通過這些反應通知同伴和拯救同伴的行為。例如一些植物受攻擊時,它會放出一些化學物質(氣體),接收到這些物質的同種植物也會作出相同的反應。
3. 這些化學物質效果各異,有些可令攻擊者中毒,有些可吸引具攻擊性的昆蟲過來以驅趕攻擊者。例如植物會釋出咖啡因吸引蜜蜂保護自己。
4. 德國波昂大學的研究指出植物放出氣體並發出一些人類無法聽見的聲音的行為等同人類的哭泣。當花、草青瓜受傷時會有這些反應。而美國密蘇里大學的研究進一步指出,當在植物前播放毛蟲吃它的同類的聲音,它們也會"哭泣",表示植物有分辨、認知同伴慘遭毒手的能力。
5. 植物縱然沒腦,但也有智能的表現,例如改變生長的方向繞過障礙物;在受到昆蟲襲擊時通知同伴等。
6. 通過追蹤含放射性碳元素的肥料的粒子流向,研究員發現樹木會和30平方米內的其他樹形成互相溝通的網絡,並利用它們的根把養份輸送到幼小的樹木,直至它長得夠高,能進行光合作用為止。(可比擬人類育嬰)
個人感想:
沒有生物傾向追求死亡,所有生物都為了生存而努力,一些總是以素食者自居,高高在上地批評其他人食肉殘忍的時候,只不過是他們無視了植物的叫聲,或者冤枉植物沒有痛覺,既然要選擇性無視植物的想法,那何不乾脆點,君子遠刨廚就好了吧。
2015年10月7日 星期三
[程式/Python] 俄羅斯方塊 Tetris
之前在Codecademy看完了python的課程後,想看看自己理解了多少,於是找了MIT的Python Course的功課和Project來做,這幾天沒發文就是去寫程式了,目前己完成所有Project。
其中一個我覺得很有趣的是自製 俄羅斯方塊 遊戲,我把它打包成執行檔了,載點如下:
>>俄羅斯方塊 下載<<
下載 俄羅斯方塊.rar 後,解壓縮並運行tetris.exe進行遊戲,其中會出現一個黑色畫面不用理會,玩完後關了它就好。
控制:
←↓→:移動方塊
↑:轉動方塊
空白鍵:直接落下
當遊戲進行到後期,畫面更新速度會加快,然後就會不定期出現一些Bug來阻礙大家遊玩∠( ᐛ 」∠)_,有發現的話請幫忙回報,我能處理的都會處理。(不過很多不是我的code有問題,似乎是Graphics Module的問題,這個我沒法處理)
完成這些Project的難點是Template都是用Python2寫的,我要把它改寫成Python3的格式,畢竟我也是一個月前第一次接觸Python,2和3的分別寫在不太熟識,結果很多時間花在翻譯code。
另外我也有完成 康威生命遊戲 ,不過這個好像沒那麼有趣所以不貼了。
遊戲畫面:
其中一個我覺得很有趣的是自製 俄羅斯方塊 遊戲,我把它打包成執行檔了,載點如下:
>>俄羅斯方塊 下載<<
下載 俄羅斯方塊.rar 後,解壓縮並運行tetris.exe進行遊戲,其中會出現一個黑色畫面不用理會,玩完後關了它就好。
控制:
←↓→:移動方塊
↑:轉動方塊
空白鍵:直接落下
當遊戲進行到後期,畫面更新速度會加快,然後就會不定期出現一些Bug來阻礙大家遊玩∠( ᐛ 」∠)_,有發現的話請幫忙回報,我能處理的都會處理。(不過很多不是我的code有問題,似乎是Graphics Module的問題,這個我沒法處理)
完成這些Project的難點是Template都是用Python2寫的,我要把它改寫成Python3的格式,畢竟我也是一個月前第一次接觸Python,2和3的分別寫在不太熟識,結果很多時間花在翻譯code。
另外我也有完成 康威生命遊戲 ,不過這個好像沒那麼有趣所以不貼了。
遊戲畫面:
2015年10月5日 星期一
[數學] 7的倍數判斷法(連證明)
網上很多人問7的倍數怎判斷,很多人知道方法但不知道怎證明,而且提不出百位數的判斷法,這個問題只要用模除就能很易證明,就結果而言,四位數以上的7的倍數可以這樣判斷:
設有四個數位以上的大數,從個位開始,每三個數位分成一組,最後一組即使不夠三位也自成一組,然後各組梅花間竹地進行加減,所得數如是7的倍數,則該大數為7的倍數。
通例:$abcdefg$是否7的倍數?
先將大數從個位開始分成三個數位組,
$a$ | $bcd$ | $efg$
然後從尾至頭梅花間竹地進行加減
$efg-bcd+a$,如此數是7的倍數,則$abcdefg$是7的倍數。
實例:
$6855448572$是否7的倍數?
先將大數從個位開始分成三個數位組,
$6$ | $855$ | $448$ | $572$
然後從尾至頭梅花間竹地進行加減
$572-448+855-6=973$
因為$973=7 \times 139$,所以 $6855448572$是7的倍數
驗算:
$6855448572=7 \times 979349796$
證明:
首先$A$ $mod$ $B$是指$A$除以$B$的餘數。
引用定理
1. $(A+B)$ $mod$ $C = [(A$ $mod$ $C) + (B$ $mod$ $C)]$ $mod$ $C$
2. $(A \times B)$ $mod$ $C = [(A$ $mod$ $C) \times (B$ $mod$ $C)]$ $mod$ $C$
及事實
3. $1000$ $mod$ $7=-1$
對於大數 $abcdefg$,
$abcdefg=a \times 1000 \times 1000 + bcd \times 1000 +efg$
所以$abcdefg$ $mod$ $7$
$= [(a \times 1000 \times 1000)$ $mod$ $7$ $+ (bcd \times 1000)$ $mod$ $7$ $ +efg]$ $mod$ $7$
$= [(a \times (-1)\times (-1))$ $mod$ $7$ $+ (bcd \times (-1))$ $mod$ $7$ $ +efg]$ $mod$ $7$
$= a-bcd+efg$ $mod$ $7$
$= efg-bcd+a$ $mod$ $7$
如果$abcdefg$是7的倍數,$abcdefg$ $mod$ $7= (efg-bcd+a)$ $mod$ $7=0$
三位數則這樣判斷:
百位數除7的餘數乘2後和百位以內的尾數相加,如答案是7的倍數則該三位數是7的倍數。
通例:$abc$是否7的倍數?
先將$a$除以7,得餘數$r$,百位以內的尾數為$bc$,然後計算
$2r+bc$,如此數是7的倍數,則$abc$是7的倍數。
實例一:
$574$是否7的倍數?
先將$5$除以7,得餘數$5$,百位以內的尾數為$74$,然後計算
$2 \times 5+74=84=7 \times 12$,此數是7的倍數,則$574$是7的倍數。
驗算:
$574=7 \times 82$
實例二:
$826$是否7的倍數?
先將$8$除以7,得餘數$1$,百位以內的尾數為$26$,然後計算
$2 \times 1+26=28=7 \times 4$,此數是7的倍數,則$826$是7的倍數。
驗算:
$826=7 \times 118$
證明(這邊寫簡化點,有點累):
$abc$ $(mod$ $7)$
$= a \times 100 +bc $ $(mod$ $7)$
$= a$ $mod$ $7$ $\times 100$ $mod$ $7$ $+bc $ $(mod$ $7)$
$= r \times 2 +bc $ $(mod$ $7)$
$= 2r+bc $ $(mod$ $7)$
不過百位數直接除也不難就是了,而且活用減700和減70的話很易就能把數值縮得很小。
設有四個數位以上的大數,從個位開始,每三個數位分成一組,最後一組即使不夠三位也自成一組,然後各組梅花間竹地進行加減,所得數如是7的倍數,則該大數為7的倍數。
通例:$abcdefg$是否7的倍數?
先將大數從個位開始分成三個數位組,
$a$ | $bcd$ | $efg$
然後從尾至頭梅花間竹地進行加減
$efg-bcd+a$,如此數是7的倍數,則$abcdefg$是7的倍數。
實例:
$6855448572$是否7的倍數?
先將大數從個位開始分成三個數位組,
$6$ | $855$ | $448$ | $572$
然後從尾至頭梅花間竹地進行加減
$572-448+855-6=973$
因為$973=7 \times 139$,所以 $6855448572$是7的倍數
驗算:
$6855448572=7 \times 979349796$
證明:
首先$A$ $mod$ $B$是指$A$除以$B$的餘數。
引用定理
1. $(A+B)$ $mod$ $C = [(A$ $mod$ $C) + (B$ $mod$ $C)]$ $mod$ $C$
2. $(A \times B)$ $mod$ $C = [(A$ $mod$ $C) \times (B$ $mod$ $C)]$ $mod$ $C$
及事實
3. $1000$ $mod$ $7=-1$
對於大數 $abcdefg$,
$abcdefg=a \times 1000 \times 1000 + bcd \times 1000 +efg$
所以$abcdefg$ $mod$ $7$
$= [(a \times 1000 \times 1000)$ $mod$ $7$ $+ (bcd \times 1000)$ $mod$ $7$ $ +efg]$ $mod$ $7$
$= [(a \times (-1)\times (-1))$ $mod$ $7$ $+ (bcd \times (-1))$ $mod$ $7$ $ +efg]$ $mod$ $7$
$= a-bcd+efg$ $mod$ $7$
$= efg-bcd+a$ $mod$ $7$
如果$abcdefg$是7的倍數,$abcdefg$ $mod$ $7= (efg-bcd+a)$ $mod$ $7=0$
三位數則這樣判斷:
百位數除7的餘數乘2後和百位以內的尾數相加,如答案是7的倍數則該三位數是7的倍數。
通例:$abc$是否7的倍數?
先將$a$除以7,得餘數$r$,百位以內的尾數為$bc$,然後計算
$2r+bc$,如此數是7的倍數,則$abc$是7的倍數。
實例一:
$574$是否7的倍數?
先將$5$除以7,得餘數$5$,百位以內的尾數為$74$,然後計算
$2 \times 5+74=84=7 \times 12$,此數是7的倍數,則$574$是7的倍數。
驗算:
$574=7 \times 82$
實例二:
$826$是否7的倍數?
先將$8$除以7,得餘數$1$,百位以內的尾數為$26$,然後計算
$2 \times 1+26=28=7 \times 4$,此數是7的倍數,則$826$是7的倍數。
驗算:
$826=7 \times 118$
證明(這邊寫簡化點,有點累):
$abc$ $(mod$ $7)$
$= a \times 100 +bc $ $(mod$ $7)$
$= a$ $mod$ $7$ $\times 100$ $mod$ $7$ $+bc $ $(mod$ $7)$
$= r \times 2 +bc $ $(mod$ $7)$
$= 2r+bc $ $(mod$ $7)$
不過百位數直接除也不難就是了,而且活用減700和減70的話很易就能把數值縮得很小。
2015年10月1日 星期四
[感想] 當北京的藍天被毒霧籠罩,香港用煙火遮蓋藍天
北京的日常
香港節日煙花
國慶本是該高慶的日子,但放煙花除了該死之外真不知有甚麼好處。
據悉今天國慶煙花浪費了八百萬公帑,也就是如果拿出來派的話,香港每人可收萬多元,大約就是香港人收入中位數左右,等於一半香港人的一個月花紅,這煙花一燒就等於燒了你一萬幾千。香港的行政長官等政要有一堆民生問題未解決,卻排排座浪費寶貴的時間在看煙花,而且還在收人工,你說該不該死?
錢是小事,健康是大事。高中化學就有教到火焰的顏色是和元素有關,而且那些無一不是金屬,而燒得不管完不完全,都會留下大量懸浮粒子危害健康。美國的環保局也建議老人、小朋友和有心臟病、肺病的人不要在下風位看煙花,而那些懸浮粒子還可維持在空中半天至一天 [1]。(不過誰能預知當日風向呢?) 也就是這些粒子的確有害健康。在北京,乾淨的空氣買少見少;在香港,政府帶頭跟進北京,不是科研或經濟方面,而是空氣污染,你說該不該死?
一年365日,吸幾天煙對健康也沒多大影響,但為了看煙花而賠上命的話,似乎更是問題了。香港的南丫四號,富士まつり2015意外,還有煙花廠爆炸之類的事故已不是第一次發生,玩火藥自然有其風險,而根據大數法則,玩的人夠多就一定會出人命,到底要慶祝甚麼這麼重要,重要到人命都要奉上?或者有些人反駁說:進食也有風險,吃的人夠多就會有人噎死,難道要因噎廢食?問題是人要存活就不得不吃東西,可是到底有甚麼大事,大得就算有機會死人也不得不放煙花?支持放煙花的人(有需求就有市場),等同間接殺死所有和煙花有關的意外喪生者,你說該不該死?
代替放煙花的活動可以有很多,為何人們堅持要為了看那一瞬的火光,浪費大量時間、金錢,賠上人命、健康在這種毫無建樹的事情上?
註:
[1] http://time.com/3943702/fourth-of-july-fireworks-pollution/ 這報導還提供了一些煙火污染的數據
[轉貼/英文] 同字首詞彙表:Pre-(前,之前)
preamble(前言)
precaution(預防措施)【caution(謹慎n., 告誡v.)】
precede(先於...)
precious(珍貴的)
precise(精確的)
predicate(斷言)【indicate(表明,示意,指着)】
predict(預測)【verdict(〔陪審團/當權者作出的〕裁決,決定);
verify(證實,核實〔某事〕)version(樣式,版本)】
verify(證實,核實〔某事〕)version(樣式,版本)】
prefer(更喜歡)【refer to(提到,參考,把…歸因於)】
prehistoric(有歷史記載以前的)【history(歷史)】
prejudice(偏見,不利於)【judge(認為,判斷,斷定,評價,法官)】
premiere(初次上演)
prepare(準備)
President(總統,校長)【resident(居民n., 居住在[+in])】
presume(認為);presume to(擅自)
prevent(預防)【invent(發明,捏造)】
preview(預習,預看,(戲劇,影片,展覽會等的)試演,試映,預展n./v.)
【review(回顧,檢查,評論n./v.)】
previous(以前的)
訂閱:
文章
(
Atom
)